Home · Overview · Users Guide · Reference Guide

Final State Particle Generation

Sartre generates processes of the form e p → e' p' V and e A → e' A' V where V can be any vector meson. This process is unique in that it allows to almost completely determine the final state particles (e', A' or p', and V) given t, W, and Q.

The energies of the beam particles (e and p or A) are input to the generator and the event generator delivers t, W, and Q and with that also y and x. This input is sufficient to derive the 4-momenta of the final state particles, e' p' and V. Below we outline the underlying calculations that are implemented in the class ExclusiveFinalStateGenerator used by class Sartre.

In what follows the 4 vectors are written in bold.

Input

• Incoming electron: q = (E_e, 0, 0, q_z)
• Incoming proton: p = (E_p, 0, 0, p_z)
• s, t, x, y, Q, W

The beam electron comes from the right, meaning q_z is negative, the proton beam is coming from the left, meaning it has positive p_z.

Scattered Electron

The scattered electron momentum q' can be calculated as:

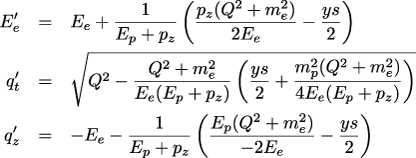
However, in order to generate a true 4-momentum we need to select an azimuthal angle. This doesn't change q_t or q_z so we have freedom here. Hence φ is chosen randomly (flat in [0, 2π[).

So this gives us the final value: q' = (E'_e, q'_t · sin φ, q'_t · cos φ, q_z).

Virtual Photon

Also the 4-momentum of the virtual photon is straightforward:

Scattered Proton

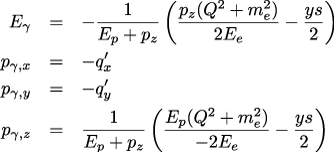
This is not a as trivial and I could not find a pure analytical solution. Here is how it goes:

From the definition of t = (p-p')² we get directly:

.

We also have the more or less trivial equations (again using a random φ):

The issue is E'. Once it is known the others are determined as well. Here it helps that there is only one generated particle, the vector meson, with a well defined mass m_V.

p_γ and p are known. We have 3 unknowns (E', p_z', and p_t') and 3 equations. Unfortunately the equations are non-linear and have no analytical solution. In the class ExclusiveFinalStateGenerator a root finder algorithm (Brent method) is used to solve the equation. With E' known, the momenta can be directly calculated. Note, that finding the correct E' is not trivial and requires additional calculation to limit the search to the kinematically valid.

Vector Meson

The 4-momentum of the vector meson is simply:

p_V = (p + q - q' - p')

$$ The actual implementation is of course a bit more complex but the above reflects the basic idea.